aez-notes

Buffon's Needle

A table of infinite expanse has inscribed on it a set of parallel lines spaced \(2a\) units apart. A needle of length \(2l\) (smaller than \(2a\)) is twirled and tossed on the table. What is the probability that when it comes to rest it crosses a line?

We describe the position of the needle by the height of the midpoint and the angle. Let 0 height be between two lines and the midpoint be at height \(x\). It is sufficient to consider positions of the midpoint \(x \in [0,a]\) and angle \(\theta \in [0,\pi/2]\). We assume \(x\) and \(\theta\) have a uniform distributions over their domain. Under this setting, the highest point of the needle is at \(x + l \cos \theta\). The following figure illustrates the set up of the problem

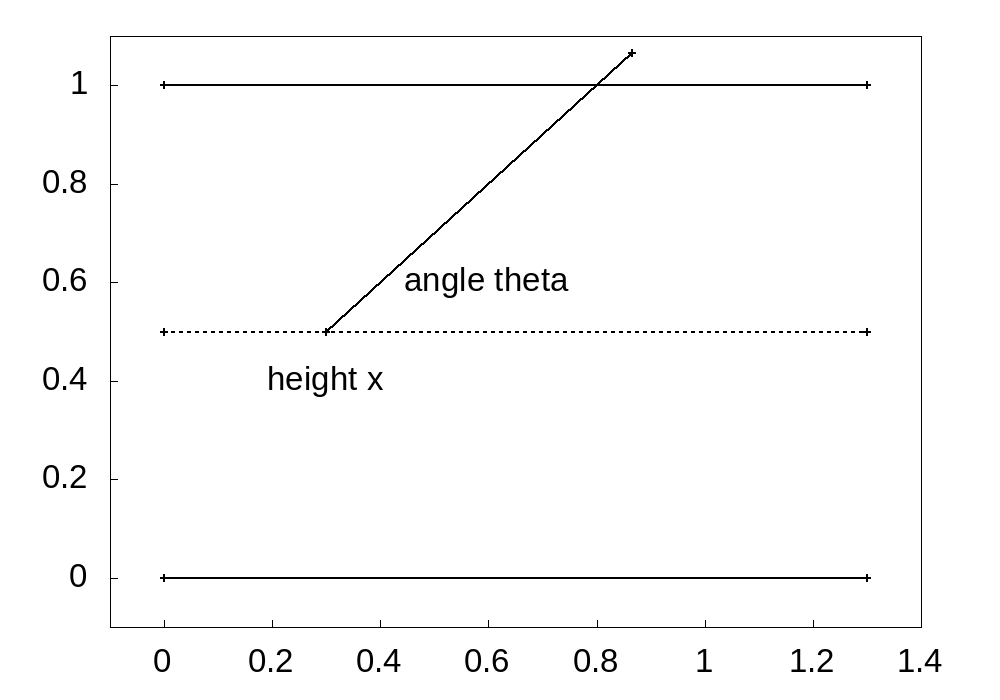
and region of parameter space that corresponds to the needle crossing the line.

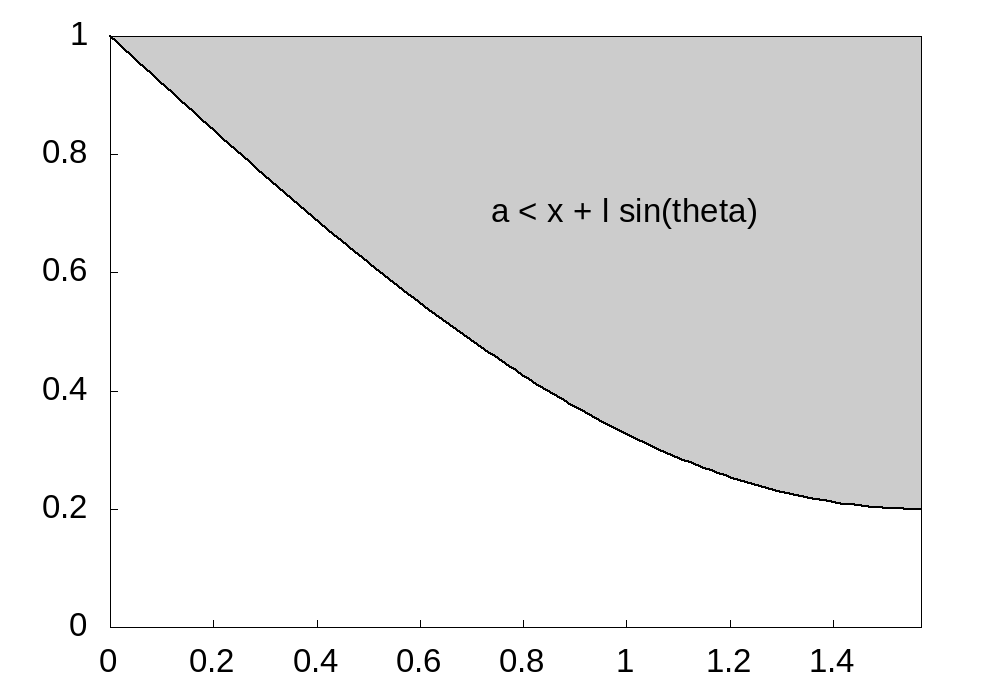
Then a simple integral shows the solution

\[ \frac{2l}{a\pi} \]

load(draw)$

a : 1;
l : 0.8;
x : a - 0.5;
th : %pi / 4;

h : 1.3;

draw(
  gr2d(
    border = false,
    color = black,
    line_width = 2,
    points_joined = true,
    line_type = dashes,
    points([0,h],[0,0]),
    line_type = solid,
    points([0,h],[a,a]),
    points([0.3,0.3 + l * cos(th)],[x,x + l * sin(th)]),
    line_type = dots,
    points([0,h],[x,x]),
    font = "Arial",
    font_size = 25,
    label(["height x", 0.3, x - 0.1]),
    label(["angle theta", 0.6, x + 0.1]),
    xrange      = [-0.1,h + 0.1],
    yrange      = [-0.1,a + 0.1]
    )
  )$

draw_file(
  terminal = 'png,
  file_name = "problem-53-a",
  dimensions = [1000,700])$

kill(x, th, h);

draw(
  gr2d(
    border = false,
    fill_color = grey80,
    x_voxel = 20, y_voxel = 20,
    region(a < x + l * sin(th), th, 0, %pi / 2, x, 0, a),
    color = black,
    line_width = 2,
    explicit(a - l * sin(th), th, 0, %pi / 2),
    font = "Arial",
    font_size = 25,
    label(["a < x + l \sin(\theta)", 1.0, 0.7])
    )
  )$

draw_file(
  terminal = 'png,
  file_name = "problem-53-b",
  dimensions = [1000,700])$

kill(all);

total_area : a * %pi / 2;
sol : l * integrate(sin(th), th, 0, %pi / 2) / total_area;

print(sol);
/*
 2 l
-----
%pi a
*/