aez-notes

Random Quadratic Equations

What is the probability that the quadratic equation

\[ {x}^{2} + 2 b x + c = 0 \]

has real roots?

Recalling the quadratic equation we find that the probability is \(P({b}^{2} > c)\) for whatever measure is used to generate the coefficients. We can draw a picture of the region of the plane which has real roots.

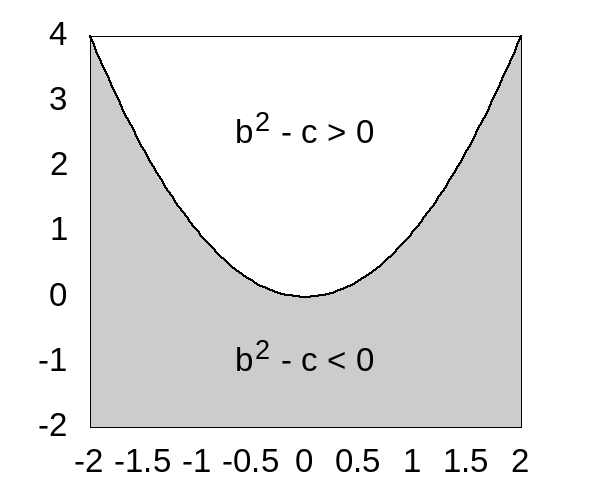
load(draw)$

draw(
  gr2d(
    border = false,
    fill_color = grey80,
    x_voxel = 20, y_voxel = 20,
    region(b^2 > c, b, -2, 2, c, -2, 4),
    color = black,
    line_width = 2,
    explicit(b^2, b, -2, 2),
    font = "Arial",
    font_size = 25,
    label(["b^2 - c > 0", 0, 2.5]),
    label(["b^2 - c < 0", 0, -1])
    )
  )$

draw_file(
  terminal = 'png,
  file_name = "problem-50")$