aez-notes

Probabilities of Matches

Under the conditions of the previous matching problem, what is the probability of exactly \(r\) matches?

To compute the probability of \(r\) matches among \(n\) cards, observe that this is the same as the number of ways to choose \(r\) of \(n\) as being matched and the number of ways the remaining cards can all not match divided by the \(n!\) possible orderings. The number of ways \(j\) items can be arranged without any in its original position is the \(j\)-th number of derangments.

load(distrib)$

derangement(n) := round(factorial(n) / %e);

f(r, n) := binomial(n, r) * derangement(n - r) / factorial(n);

f_approx(r) := pdf_poisson(r, 1);

The exact solution is well approximated by a Poisson distribution as shown in the following figure.

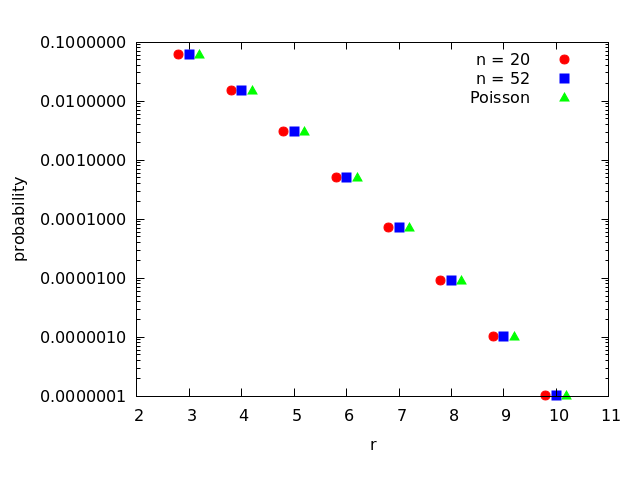
p_x : makelist(r, r, 3, 10);
p_x_1 : makelist(r-0.2,r,3,10);
p_y_1 : map(lambda([x], f(x, 20)), p_x);
p_x_2 : makelist(r,r,3,10);
p_y_2 : map(lambda([x], f(x, 52)), p_x);
p_x_3 : makelist(r+0.2,r,3,10);
p_y_3 : map(lambda([x], f_approx(x)), p_x);

plot2d([[discrete, p_x_1, p_y_1],
        [discrete, p_x_2, p_y_2],
        [discrete, p_x_3, p_y_3]],
  [style, points],
  [color, red, blue, green],
  [legend, "n = 20", "n = 52", "Poisson"],
  [xlabel, "r"],
  [ylabel, "probability"],
  logy,
  [png_file, "./problem-46.png"]
);