aez-notes

The Broken Bar

A bar is broken at random in two places. Find the average size of the smallest, of the middle-sized, and of the largest pieces.

Without loss of generality we can order the pieces by size and assume that the breaks occur at locations \(a\) and \(b\) on a bar of unit length with the conditions that

\(a < b - a\) so that the first piece is smaller than the second,
\(b - a < 1 - b\) so that the second piece is smaller than the third.

The distribution of \((a,b)\) is uniform over the permissible values,

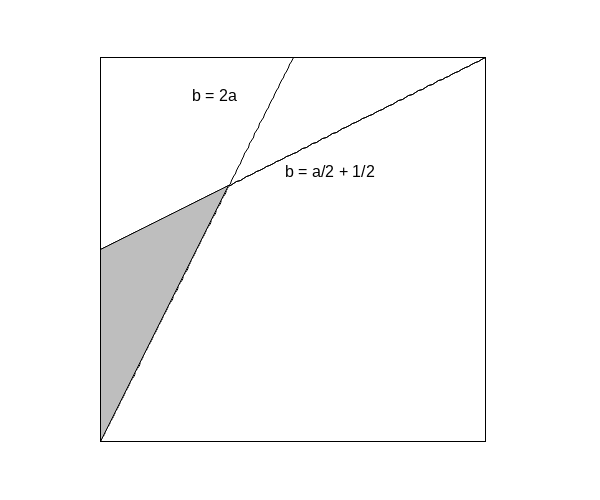
Then we can just ask maxima to do the relevant integrals.

c : integrate(integrate(1, b, 2*a, (1 + a) / 2), a, 0, 1/3);
print(c);
/*
1
--
12
*/

mean_len(x) :=
integrate(
  integrate(x / c, b, 2*a, (1 + a) / 2),
  a, 0, 1/3
  );

m_shortest_length : mean_len(a);
print(m_shortest_length);
/*
1
-
9
*/

m_middle_length : mean_len(b-a);
print(m_middle_length);
/*
5
--
18
*/

m_longest_length : mean_len(1-b);
print(m_longest_length);
/*
11
--
18
*/

print(m_shortest_length + m_middle_length + m_longest_length);
/*
1
*/

So this just reduces to two integrals and the third once can be obtained from the results of the first two.

draw2d(
  fill_color = white,
  color = black,
  rectangle([0,0],[1,1]),
  color = black,
  line_type = dashes,
  label(["b = 2a", 0.3, 0.9]),
  explicit(2 * x, x, 0, 1/2),
  label(["b = a/2 + 1/2", 0.6, 0.7]),
  explicit(1/2 * (1 + x), x, 0, 1),
  explicit(1/2 * (1 + x), x, 0, 1),
  fill_color = grey,
  polygon([[0, 0], [0, 1/2], [1/3, 2/3]]),
  <<style-and-writeout>>
  )$

xrange      = [-0.1,1.1],
yrange      = [-0.1,1.1],
axis_bottom = false,
axis_left = false,
axis_top = false,
axis_right = false,
xtics = false,
ytics = false,
proportional_axes = 'xy,
file_name = "problem-43",
terminal = 'png